In Timo Nasseri’s exhibition “Nine Firmaments” he concerns himself with the topic of notation and readability. He examines the di­fficulties of transcription and the loss of knowledge through notation and its transferal back into the three-dimensional space. Nasseri’s drawing “Nine Firmaments”, which lends the show its title, as well as “Orbis Tertius” make use of illustrative elements that appear familiar to the observer. Graphic, geometric symbols, digits and letters from the fields of mathematics, cartography and astronomy are placed in a complex, yet purely intuitive, indecipherable correlation. The words, numbers and forms bear associative significance for the observer, seem to be references, but no clear sense can be made of them, despite the fact that these notations originally serve to designate and preserve information and knowledge and make them accessible. Nasseri questions the vocabulary of characters that visually has become so commonplace to us by creating his own fantastical worlds of characters, captivating in their minuteness and precision, but also puzzling to the observer. They echo Nasseri’s drawing block “O Time Thy Pyramids”. Intellectually they reference Jorge Luis Borges’ literary work “The Library of Babel” (1941), in which every possible combination of letters and words is preserved in an infinite library and thus all knowledge is represented. As it contains every possible combination, it seems cacophonous and indecipherable. However, it may be that just one deciphering code is missing for a possible translation, similarly to the keys needed to understand mathematical formulas.

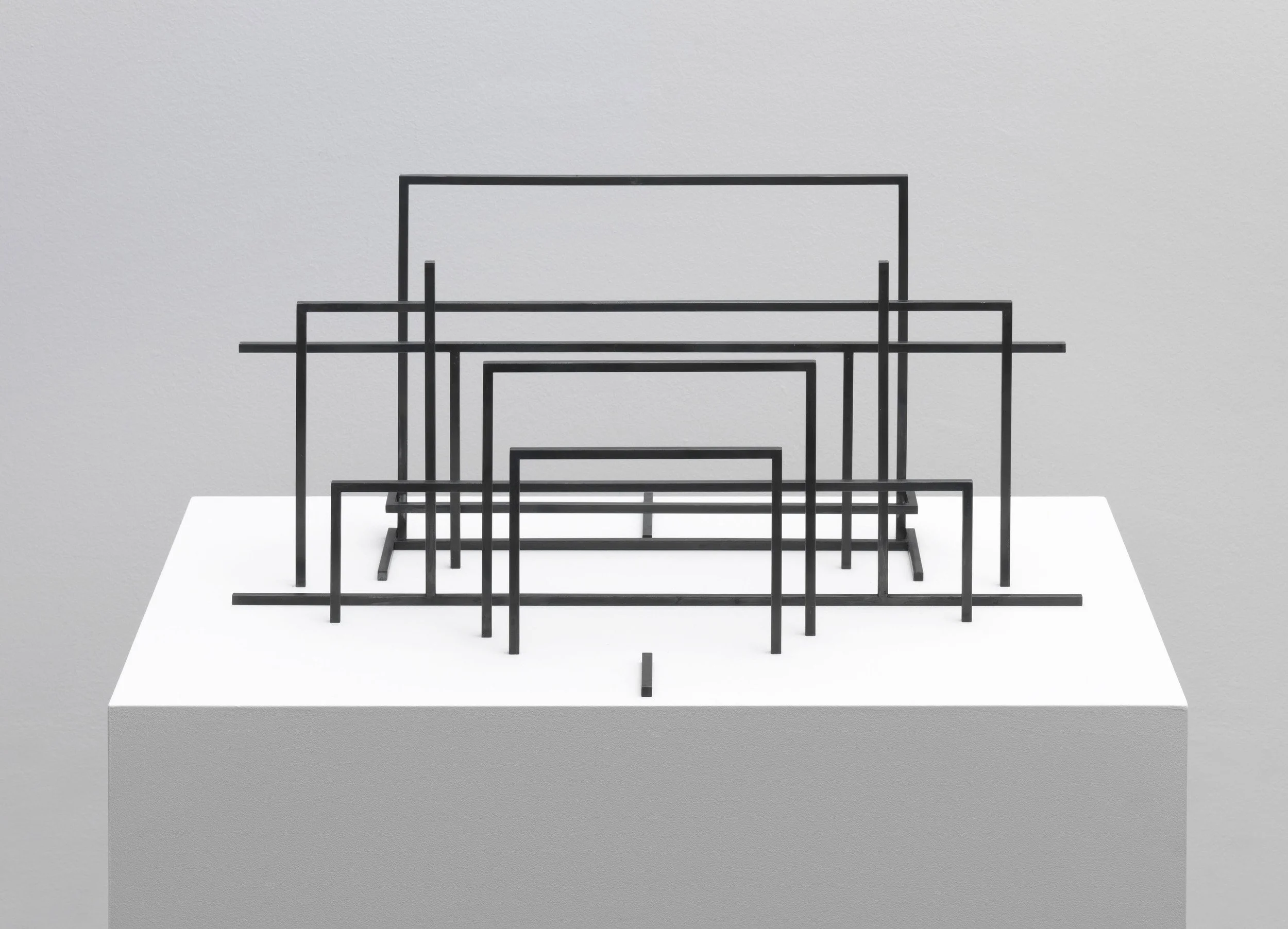
The sculptural works presented in the exhibition stem from these drawings in the “O Time Thy Pyramids” series. They continue the ideas inherent in them, attempting to recreate the legibility in the three-dimensional of that which is illegible or has been lost in the two-dimensional space, such as the volumes of bodies. As such, they are derivatives, back-translations and interpretations of a notation in the three-dimensional realm.

The resulting space-consuming installation consists of several individual sculptures, which Timo Nasseri links into a related, modular reference system: clear, geometric, abstract shapes in materials such as brass, wood, black, powder-coated steel or thread.

“Pion” (2015), which is part of the ensemble, consists of various adjustable spheres rotating around one another, as in a sky model or globe, and a network of stretched threads that seem to form curves. As in the centrally positioned sculpture, the curves arise from straight lines staggered such that they rotate about themselves and therefore appear to form curves. Here Nasseri was initially inspired, as with the “Mesh” sculptures, by geometric drawings by Jakob Steiner (1796 – 1863), a Swiss mathematician who sought a way to describe cone shapes in drawings using parabolas. Nasseri addresses the opposite question, the transfer of two-dimensional structures back into the three-dimensional space and the change a system undergoes when a dimension is added or subtracted. Both his drawings and sculptures are frequently based on geometric systems of order and the mathematical foundations of folds and ornament. The small-scale drawing block, consisting of five sheets, and the new drawing from the series “I saw a broken labyrinth” are composed of lines that become denser in some areas, then become more spaced again or overlap, thus forming visual rhythms. At points they appear to vibrate. Force fields emerge. In general in Nasseri’s work, be it two-dimensional or three-dimensional, the line plays a role in connection with the topic of infinity. As mathematically speaking a line, no matter how long, consists of an infinite number of dots, it is a placeholder for the infinite. Thus an infinite macrocosm is present in every single graphic notation of these geometric microcosms. Yet the line is also an example of our perception: The observer sees the line, but not its constituent parts, the infinite number of dots. Yet he can use it to describe the infinite in the form of words or drawings, i.e. notations.